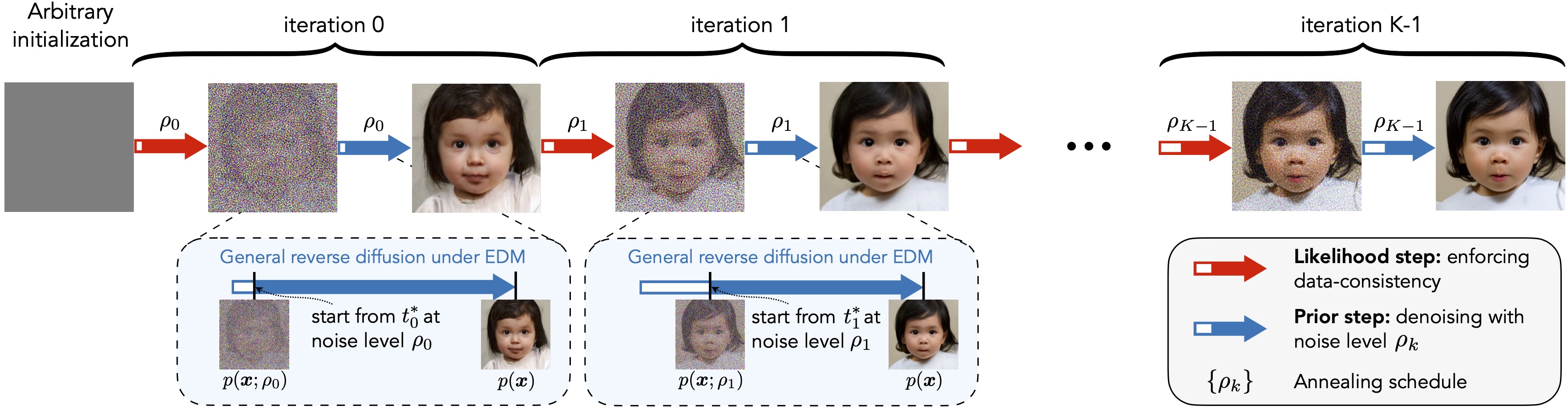
Our method alternates between a likelihood step that enforces data consistency and a prior step that solves a denoising posterior sampling problem by leveraging the Split Gibbs Sampler. An annealing schedule controls the strength of the two steps at each iteration to facilitate efficient and accurate sampling. A crucial part of our design is the prior step, where we identify a key connection to a general diffusion model framework called the EDM. This connection allows us to easily incorporate a family of state-of-the-art diffusion models as priors to conduct posterior sampling in a principled way without additional training. Our method demonstrates strong performance on a variety of linear and nonlinear inverse problems.

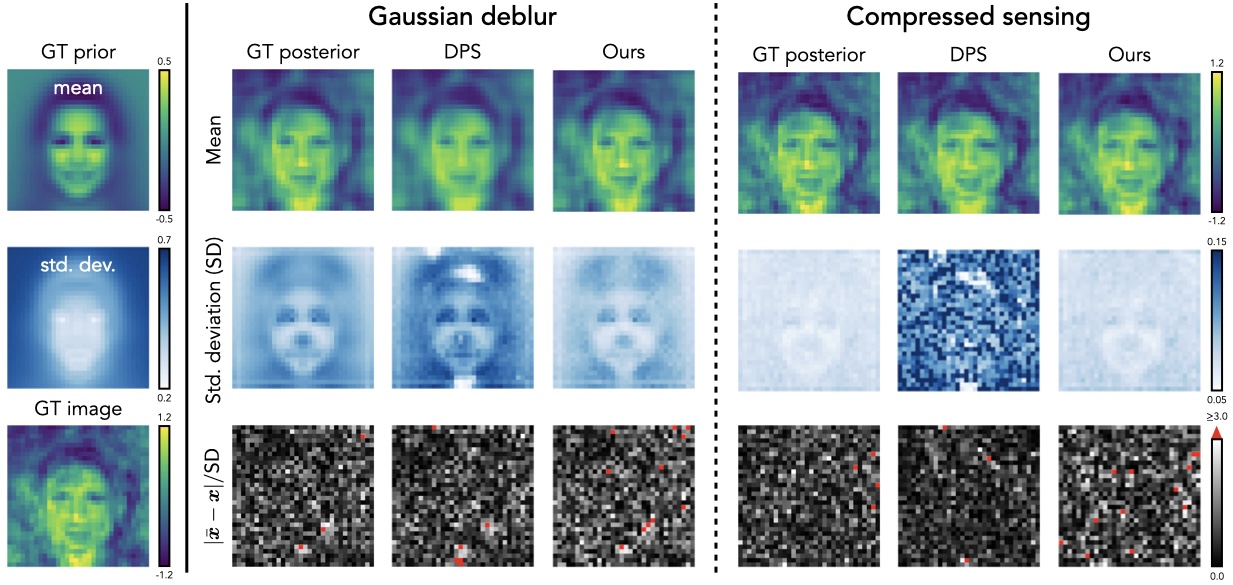
We validate the accuracy of PnP-DM on a synthetic problem where the ground truth posterior is available. PnP-DM can sample the posterior distribution more accurately than the existing method DPS.

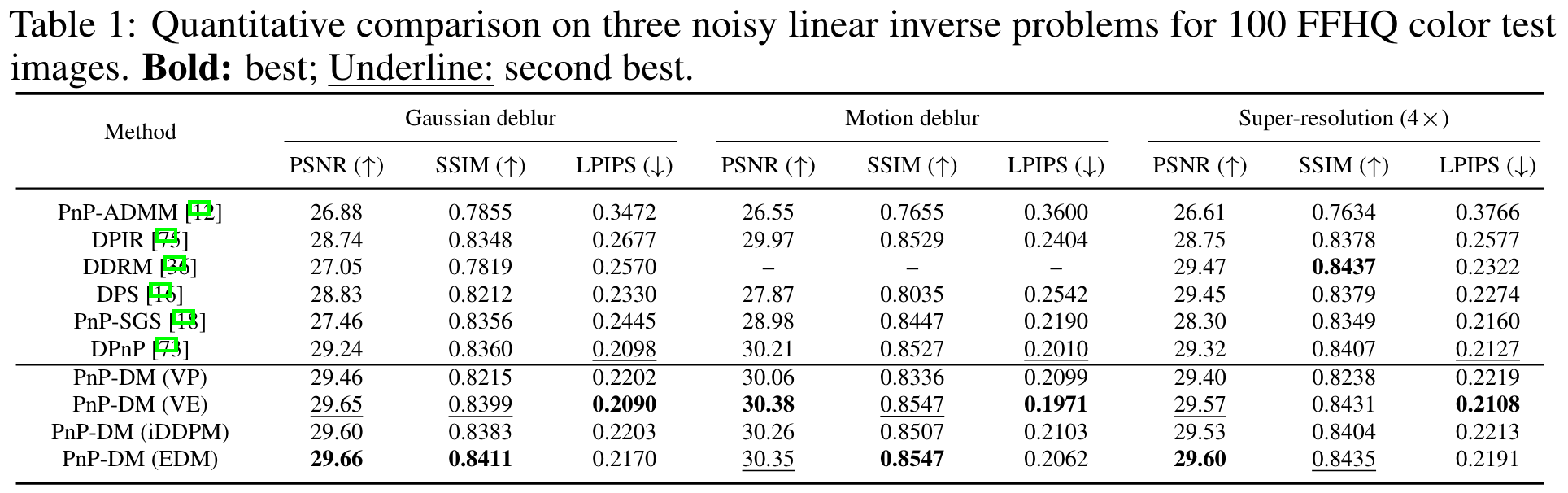
Overall, PnP-DM outperforms existing methods on linear inverse problems both numerically and visually.

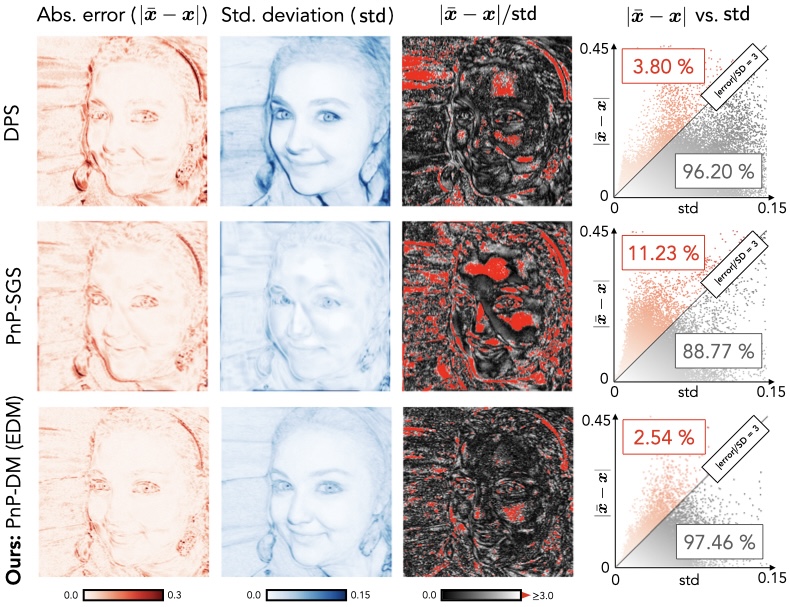
We also provide an uncertainty quantification analysis based on pixel-wise statistics for the motion deblurring problem (left 3 columns: absolute error, standard deviation, and absolute z-score with the outlier pixels in red; right column: scatter plot of absolute error versus standard deviation). Note that PnP-DM outperforms the baselines by having the lowest percentage of outliers while avoiding having overestimated per-pixel standard deviations.

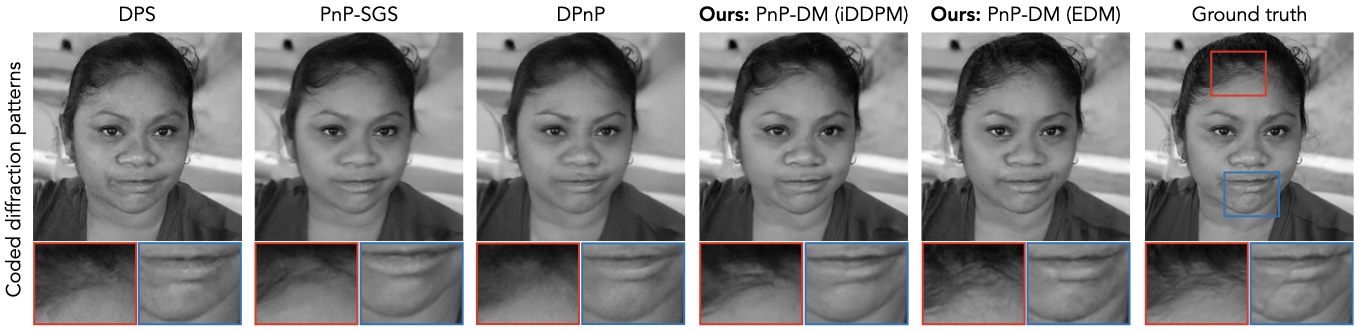
For the coded diffraction patterns (CDP) reconstruction problem, PnP-DM performs on par with DPS but outperforms other SGS-based methods.

The Fourier phase retrieval (FPR) problem is known to be a challenging nonlinear inverse problem. One challenge lies in its invariance to 180^◦ rotation, so the posterior distribution have two modes, one with upright images and another with 180^◦-rotated images, that equally fit the measurement. To increase the chance of getting properly-oriented reconstructions, we run each algorithm with four different random initializations and report the metrics for the best run. We find that PnP-DM significantly outperforms the baselines on this highly ill-posed inverse problem. As shown in (a), our method can provide high-quality reconstructions for both orientations, while the baseline methods fail to capture at least one of the two modes. We further run our method for a test image with 100 different random initialization and collect reconstructions in both orientations that are above 28dB in PSNR (90 out of 100 runs). The percentages of upright and rotated reconstructions are visualized by the pie chart in (b). With a prior on upright face images, our method generate mostly samples with the upright orientation. Nevertheless, it can also find the other mode that has an equal likelihood, demonstrating its ability to capture multi-modal posterior distributions.

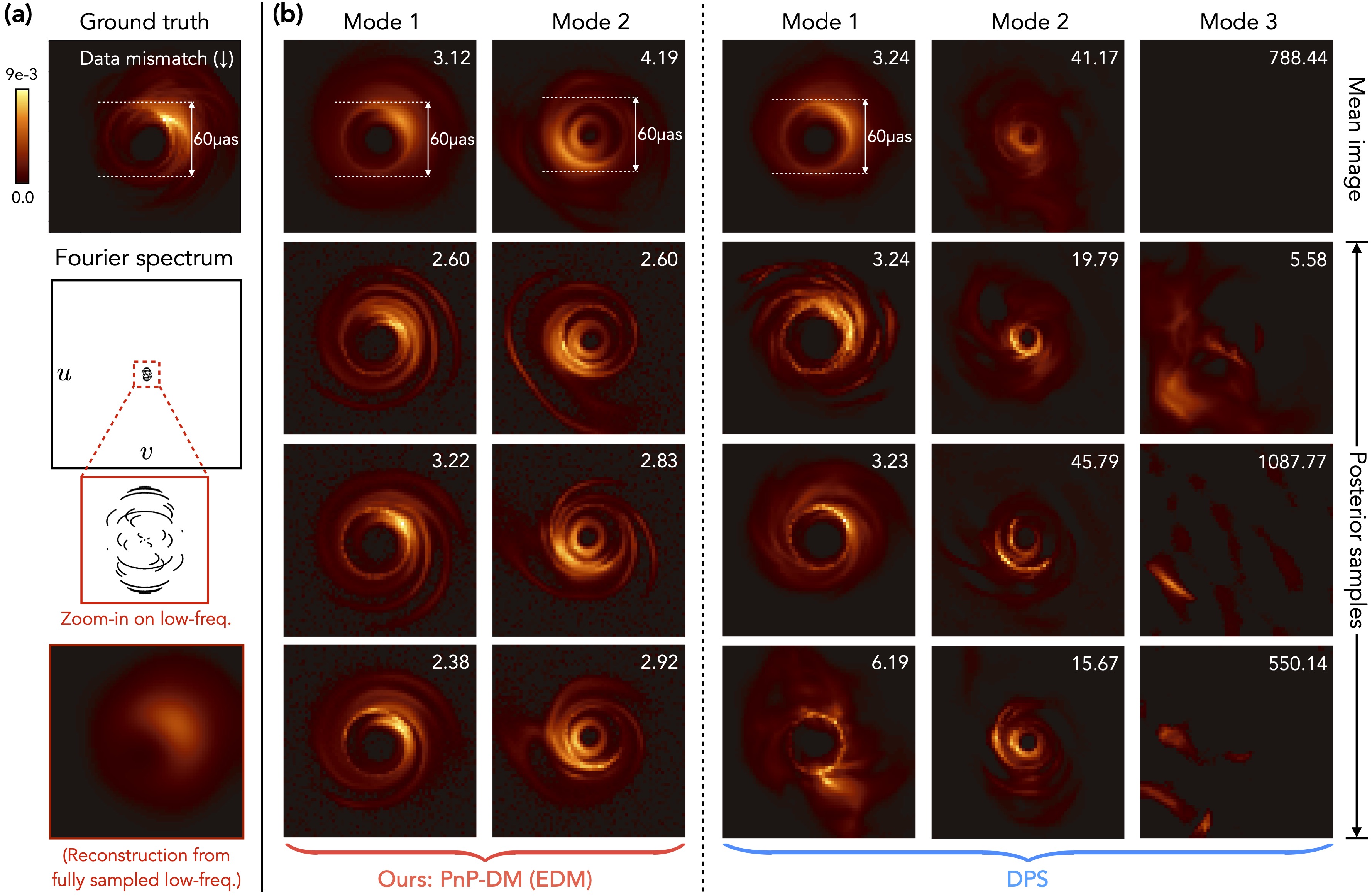
We consider a nonlinear and severely ill-posed black hole imaging problem where the prior literature has discovered two modes in the posterior distribution. Our method, PnP-DM, is compared with the conditional diffusion model baseline DPS. A metric quantifying the mismatch with the observed measurements is labeled for each sample, which should be around 2 for ideal measurement fit. Samples generated by PnP-DM exhibit two distinct modes with sharp details and a consistent ring structure, while samples given by DPS display inconsistent ring sizes and sometimes fail to capture the black hole structure entirely with samples having poor measurement fit.